
|
Application Note #G-SA1 Synchro Torque (Producing) Receivers When driving Synchro Torque Receivers, power is pulled from and against the 2 following sources: |
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
Torque receivers provide torque as a result of the interaction of the two magnetic fields introduced through these coils within the torque receiver itself. The torque receiver is considered an active load in that it works against the opposing stator coil inputs, thereby loading them to produce the torque required of its shaft. Torque is produced whenever the torque receivers shaft angle differs from the angle dictated by its 3 wire stator input. The angular difference is reflected as a voltage gradient that develops circulating currents in the stators, working against the rotors magnetic field. These opposing stator currents provide the magnetomotive force against the rotors magnetic field, to move the rotor shaft. Theoretically, when the shaft angle is positioned exactly to the angle dictated by it’s 3 wire synchro input (respective of the phasing of its rotor input); the load impedance is infinite, the shaft is nulled and the load is null. In practice however, the amplifiers outputs must still accommodate the load incurred by virtue of both the voltage and phase differentials existing between the amplifier outputs and the actual characteristics of the torque receivers imperfect stator coils. These differential effects are significant, and must be considered when specifying appropriated amplifiers for a given application. Driving Synchro Torque (producing) Receivers When driving torque receivers, the amplifier must be able to handle both: the peak transient power required to be able to drive the torque receiver to a null (close the loop), in addition to being able to supply enough steady state, continuous power to maintain the torque receiver at null, accommodating the circulating currents at the null resulting from phase shift and voltage differentials in the driven synchro, the amplifier, and the D-S converter or other synchro driving amp. When driving a Torque Receiver, like driving a servo, we are constantly attempting to null the circuit to achieve any desired position, to null a 3 wire synchro consider the voltage required at null in a 3 wire synchro format as: sine(120o)(Vm)Vm=voltage magnitude Vm for a 115V/90V L-L synchro: (.866)(90V.L-L)=78 V. L-L Vm for a 26V/11.8V L-L synchro: (.866)(11.8)=10.2 V. L-L This Vm (voltage magnitude) is the voltage that will be measured with two stator legs shorted across the remaining winding. See the following illustration “Zss:” |
|||||||||||||||||||||||
|
Fig. Zss, Driving Torque Receiver Loads |
|||||||||||||||||||||||
|
The power amplifier’s Zss (output impedance) must be low enough to drive the combined Zss of all the Torque receivers being driven, (plus the Zso of all the CT’s and CDX’s being driven off the same load (less if these are tuned)), to accommodate the peak transient power required to be able to drive the torque receiver’s shaft to a null (close the loop). Additionally, the Synchro Amplifier must be able to provide enough continuous power to accommodate the circulating currents respective of the phase shift and voltage mismatch (Vmm), required just to maintain a null. Calculating Load Impedances Required to Maintain a Null (To maintain desired position, minimum continuous current flow) The criteria used to determine the effective load impedance at null, or effectively how much power will be required just to maintain a constant position, we must consider the voltage mismatch and phase shift respective of the components used in the system.
|
|||||||||||||||||||||||
|
The active load calculations derived by these two variable differentials may be referred to as the “null wattage” or the “VA @ null required,” the power exhibited as circulating currents flowing just to maintain a null (any constant position), which is lost wattage above and in addition to the VA required of the amplifier to produce any torque. Calculating line to line “Voltage Mismatch” @ null
|
|||||||||||||||||||||||
|
The Transformer Ratio (Input to Output) tolerance of most synchro’s is typically +2%:
|
|||||||||||||||||||||||
|
*Amplifier Scale Factor Accuracy: +/-1.% |
|||||||||||||||||||||||
|
+/-3.0% voltage differential (or mismatch) can be used for nominal calculations, with 1 synchro TR and any of CCC’s Reference Powered Synchro Amplifiers. When driving a Torque Receiver, like driving a servo, we are constantly attempting to null the circuit to achieve any desired position. To null a 3 wire synchro consider the voltage required at null in a 3 wire synchro format as: sine(120o)(V.L-L) for a 115V/90V L-L synchro: (.866)(90V.L-L) = 78V.L-L When driving a synchro Torque Receiver using 115VAC reference and 90 V.L-L stators, anticipate this 3.% in synchro system tolerances, will yield a Voltage Mismatch of 2.34V. 78V.L-L(.03 System Tolerance) = 2.34V.L-L = Vmm, The following figure illustrates the power required at null (actually to satisfy the circulating currents that will be flowing) attributed to the voltage differential (magnitude error, or component mismatch) in the synchro system driving a T.R. |
|||||||||||||||||||||||
|
Fig. Vmm, voltage mismatch currents @ null |
|||||||||||||||||||||||
|
Take the magnitude of the voltage mismatch (V1-V2) over the total impedance of the circuit (output impedance of the transmitter or amplifier) (Zss=ZT) - the impedance of the Receiver (Zss=ZR). This current times the nominal voltage (78V.for 115/90V systems) represents the power flowing at null in VA or watts, just to satisfy the voltage mismatch. If multiple synchro’s are being driven, only the impedance of the receivers side needs to be changed, calculate like adding resistors in parallel: |
|||||||||||||||||||||||
|
1/R1+1/R2+1/R3=1/Total=ZSS=ZR |
|||||||||||||||||||||||
|
Sine (phase shift in degrees) (Vm) =Vme |
|||||||||||||||||||||||
|
Voltage Mismatch and Amplifier Headroom: The voltage mismatch must also be considered with respect to the negative potential of the mismatch versus the amplifiers voltage envelope, to insure there is sufficient headroom such that the negative flowing currents do not try to back feed or buck the amplifier outputs, possibly causing damage to the amplifier. This is explained in greater detail in the following section regarding large phase shifts, and includes both the tolerance of different synchro amplifiers, and the means to increase the headroom and ZSS in the system, Calculating Line to Line Phase-Shift Differential @ Null:
When reference powered amplifiers are used, the 3 wire synchro outputs are in phase shift with the reference input, the phase shift specified of the Torque Receiver being driven provides the line to line phase shift differential. Theoretically, when driving only one synchro this effect can be minimized by adding a phase shift compensation RC (Resistor Capacitor Network) in series with the rotor input of and at the source of Alternatively, adding a large capacitor in series with the Reference input of the Synchro Amplifier can be considered, but this is also requires a RC phase lead/lag network be added to the synchro or D-S converter driving the amplifier itself. Large Phase Shift Effects: Most installations specify power sufficient to accommodate the increased load required to maintain a null, respective of both the phase shift and voltage mismatch differentials required of the synchro’s employed, but the voltage tolerance especially with respect to the phase shift should be calculated to insure there is enough voltage mismatch headroom, that the negative flowing currents do not try to back feed or buck the amplifier outputs, possibly causing damage to the amplifier. Phase shift differentials can be significant, example: a typical 15TRX6a has a 20 degree phase shift, a 23TR6 is a 9.1 degrees, also consider the phase shift tolerance between like manufactured synchro’s is approx. +/-20% of that nominally specified. This is further complicated when driving multiples of differing synchro’s off of one common amplifier. When Reference Powered Synchro Amplifiers are used to drive synchro Torque Receivers having large phase shifts, the phase shift limits the peak voltages available from the pulsating power supplies, this is because the pulsating power supplies’ peak voltages are full-wave rectified, and in phase with, the reference (power) input. The peak magnitude of the voltage seen as phase shifted away from the reference is less. This makes the amplifiers effective output voltage envelope smaller, limiting or reducing the peak amplitude available on the outputs with respect to the synchro’s desired phasing. The more undesirable effect (from phase shift) is when the synchro stator signals being driven by the amp, exhibit a higher voltage (by virtue of the induced rotor voltage coupling working against the stators) than the peak voltages being produced by the amplifier. This results in a negative voltage mismatch which, is significant enough will try to back feed or buck the synchro amplifiers output stage. Calculations for the effects of Phase Shift on Synchro Amp. To calculate the circulating currents that will be flowing at null attributed to phase shift, first calculate the Voltage magnitude error, (or the voltage offset) incurred by the phase shift, over the total impedance of the circuit (output impedance of the transmitter or amplifiers ZSS = ZT) + the impedance of the |
|||||||||||||||||||||||
|
Fig. PS-(VME), Phase Shift Voltage Magnitude Error |
|||||||||||||||||||||||
|
To calculate the power that will be lost to phase shift to simply maintain a null: I (Vm) = VA Where Vm = Voltage magnitude used to Drive Synchro, Vm = for 115/90 Systems use 78V, Vm = for 26/11.8V Systems use 10.2V Vme = Voltage Magnitude Error, this voltage will be present on the driven synchro’s leads, fighting against the power amplifiers outputs, at the zero-crossings of the reference input sine wave, when the reference input is providing no instantaneous power, and likewise, the dynamic pulsating supply has no instantaneous power to transfer; at the instant of these (reference/power input) zero crossings; the amplifier is essentially driving 0V, 0 current (less mismatch), while the driven synchro inductively applies to the same signal lines its phase shifted voltage potentials. The difference between the voltage seen from the driven synchro, at the zero-crossing of the pulsating supply; must fit into the headroom tolerated by the amp. If the phase shift line to line voltage plus the mismatch exceeds the voltage mismatch headroom tolerated by the amp: the phase shift must be compensated for, or external resistors must be used, on the stator lines to increase the headroom, or both. Synchro Amplifier Headroom: The negative voltage mismatch that CCC’s Reference Powered Synchro Amp’s are designed to tolerate for 115/90V. units are as follows, (this is your headroom tolerance): 25 VA unit: 6.7 Volts/leg, (2) + 13.4 Volts across winding 50 VA unit: 2.45 Volts/leg, (2) = 4.9 Volts across winding 100 VA unit: 1.73 Volts/leg, (2) = 3.46 Volts across winding Techniques used to increase the Synchro Amplifier Headroom: 1.) Adding Load Balancing Resistors (illustrated in figure LBR) To increase the amount of negative voltage mismatch tolerated by the amp. without shutting down the outputs, the user can add large (10-20) watt resistors in series with the amplifiers synchro outputs representing up to 2-3rd’s of the synchro load being driven (represented as the ZSS “Stator impedance rotor shorted,” specified for the synchro (or synchro’s) being driven in each leg. |
|||||||||||||||||||||||
|
Load Balancing Resistors & Ph
The added resistors will effect the current flow through the synchro, the synchro signals however will still read 90 V.L-L. The higher the total line impedance, the lower the current flow at null. Though this will certainly help minimize the voltage at null, and lower the current flow. There may be a slight reduction in peak torque available on the synchro’s output shaft (when driving very large shaft loads). When driving multiple synchro loads, load sharing effects’ can and will minimize loss of torque. Occasionally, when driving several different Torque Receivers with large shaft loads, compromise may be required, and the user may have to try a couple of different load balancing resistors, or phase shift capacitors to the amp’s reference input to optimize driving the loads. When driving multiple synchro Torque Receivers, the phase shift should be apportioned respective of the ZSS rating of each synchro versus its phase shift, the larger that synchro's load (the lower its ZSS impedance), the more its effect of phase shift will burden the system. Adding Lead/Lag RC networks for phase shift compensation: If the phase shift is large, the user may add (or order with internal) a phase shift lead/lag RC (resistor/capacitor) network on the D-S converters reference input lines, and use a large capacitor on the reference input of the synchro amplifier to compensate for the average phase shift of the load driven. If a 115V, 60 Hz. synchro system is being used, start with a 10 U. 400V cap. in series with RH on the synchro amp, simply measure phase shift between S1-S3 out versus the RH-RL in, when loaded, on a dual-trace scope. The formula used to calculate the phase shift for the D-S are as follows: |
|||||||||||||||||||||||
|
tan ø = XC XC = 1 |
|||||||||||||||||||||||
|
Load Balancing Resistors & Phase Shift added to Synchro Amp. |
|||||||||||||||||||||||
|
The input impedance of the reference input specified for the D-S converter is required as part of “R” resistor component (see Data Sheets). CCC converters are available with internal phase shift. Control Transformer CT’s and CDX type Synchro’s CT’s are relatively high impedance rotary transformers that provide a single phase AC rotor output representing the sine of the difference between the absolute shaft angle of it’s rotor and it’s 3 wire stator (command) inputs. CT’s are typically coupled directly on the apparatus being controlled, providing instantaneous position feedback and control, it’s output is typically amplified to drive a servo motor direct, thus the motor automatically nulls it’s shaft to the command angle dictated by the CT’s 3 wire input. CT’s are typically driven from CX (control transmitter) or CDX (control differential transmitters). CDX’s (control differential transformers) have a 3 wire primary input, a physical rotor shaft angle input, and a 3 wire secondary output used to drive CT’s other CDX’s or even TR (Torque Receiver) inputs. The CDX output is a 3 wire synchro format representing the angular difference between the absolute shaft angle of it’s rotor input and the shaft angle command determined by it’s 3 wire synchro input. Because the CDX is used to drive other synchro’s, it’s load must be added to the loads required of all the synchro’s connected to it’s outputs, to determine the full magnitude of the load burden that will be required of it’s inputs. CDX’s are typically driven from a CX (control transmitter) or another CDX, they are used as active offsets in a synchro chain to bias their synchro inputs by the shaft angle of their rotor. Driving CT’s and CDX’s When driving CT’s or CDX’s the amplifier must be able to supply enough steady state, continuous power to drive the Zso of the load. |
|||||||||||||||||||||||
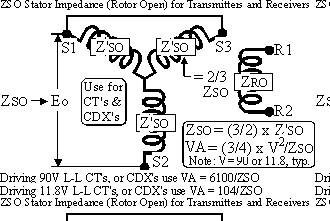 |
|||||||||||||||||||||||
Fig. ZSS, Driving Control Transformer (CT) and CDX Loads
Power Factor Correction by Tuning CT’s and CDX’s
Unlike the more resistive load requirements of Torque Receivers; CT’s and CDX’s are primarily inductive loads, whereby power factor correction can be achieved to reduce the reactive component by simply turning the loads.
CT’s and CDX’s may be turned by adding good grade, unpolarized, poly-type, high voltage tuning capacitors in a delta configuration, in parallel with the stator inputs (see illustration, use 400V. min capacitors for 90V.L-L signals).
The use of tuning capacitors can reduce the load burden to the synchro, or even a whole chain of synchro’s by as much as 50%
Fig. TC, Adding Tuning Capacitors for CT Type Loads